Iron ore rout weakens Rio Tinto

The stock of Rio Tinto Plc lost about 5%, or $1 billion of its market capitalization, last week to close at $38.94. No trophies for guessing the reason! The price of iron ore fell below $70 per ton.

This gave an opportunity for punters to hammer the stock of Rio Tinto, the world’s largest iron ore miner. There are optimists who believe that the raw material for steel industry would recovery sharply.

However, we don’t think so. In fact, we anticipate the price of iron ore and that of Rio Tinto to decline further due to the reasons mentioned below.

Last week, the price of 62% pure iron ore fines had a free fall of 8.5% to $68.04 per ton. It has been the lowest recorded price since November 2016. The extent of the decline can be understood from the fact that the price of iron ore has declined about 28% from the February high of $94.86 per ton. More importantly, the decline, as per analysts, is far from over. It may take several months before most of the stockpiles at the Chinese ports are used up by the steel mills.

Rio Tinto

There is also little possibility of an increase in demand. Construction activities are principally responsible for an increase in demand for iron ore. Recently the Chinese government has brought about another round of lending restrictions to avoid overheating of the economy. This is expected to affect construction activities in nearly 20 cities. According to Li Xinchuang, vice chairman of China Iron and Steel Association (CISA), the demand for steel is expected to decline due to a drop in construction activities.

In Indonesia, Freeport-McMoRan, the world’s low cost producer of copper, is facing problems in exporting copper concentrate, due to new restrictions laid down by the government. Rio Tinto, which owns a stake in the Grasberg mine (copper and gold) of Indonesia, is negotiating with the government and Freeport-McMoRan to resolve the issue. The stake allows Rio Tinto to claim up to 40% of the production beyond specific levels until 2021, and 40% of the entire production after 2021.

The Australian Taxation Office has slapped Rio Tinto with a notice demanding an additional tax of $379 million plus interest of $68 million for the period ranging from 2010 to 2013. The demand was based on assessments related to transfer pricing of commodities to Rio Tinto’s hub in Singapore. The company has stated that it would pay 50% of the demand and simultaneously challenge the taxation mechanism. Out of the $7.1 billion paid as tax in 2014, $3.3 billion was paid to the Australian government in the form of tax and royalties.

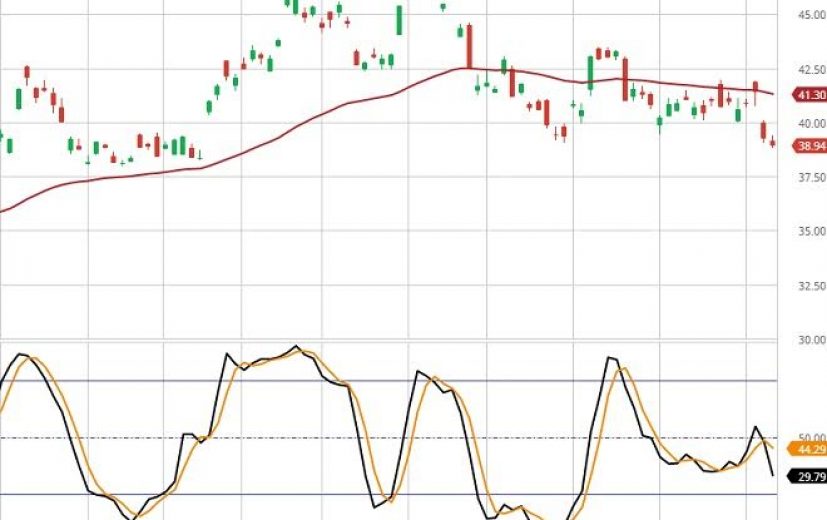
The price chart indicates that the stock has broken the major support at 41. Additionally, the stock has fallen below the 50-day moving average as well. The weakness in the stock is also pointed by the declining stochastic oscillator. Thus, a downtrend can be anticipated in the share price of Rio Tinto.

A binary trader can gain from the downtrend by purchasing a put option contract with a validity period of one week. The trader will also have better chances of winning, if the investment is made at a time the stock trades near $40 in the NYSE.

---